The Linked List
The first data structure we will be looking at is the linked list, and with good reason. Besides being a nearly ubiquitous structure used in everything from operating systems to video games, it is also a building block with which many other data structures can be created.
In a very general sense, the purpose of a linked list is to provide a consistent mechanism to store and access an arbitrary amount of data. As its name implies, it does this by linking the data together into a list.
Before we dive into what this means, let’s start by reviewing how data is stored in an array.

As the figure shows, array data is stored as a single contiguously allocated chunk of memory that is logically segmented. The data stored in the array is placed in one of these segments and referenced via its location, or index, in the array.
This is a good way to store data. Most programming languages make it very easy to allocate arrays and operate on their contents. Contiguous data storage provides performance benefits (namely data locality), iterating over the data is simple, and the data can be accessed directly by index (random access) in constant time.
There are times, however, when an array is not the ideal solution.
Consider a program with the following requirements:
- Read an unknown number of integers from an input source (
NextValuemethod) until the number 0xFFFF is encountered. - Pass all of the integers that have been read (in a single call) to the
ProcessItemsmethod.
Since the requirements indicate that multiple values need to be passed to the ProcessItems method in a single call, one obvious solution would involve using an array of integers. For example:
1 |
void LoadData() |
2 |
{
|
3 |
// Assume that 20 is enough to hold the values.
|
4 |
int[] values = new int[20]; |
5 |
for (int i = 0; i < values.Length; i++) |
6 |
{
|
7 |
if (values[i] == 0xFFFF) |
8 |
{
|
9 |
break; |
10 |
}
|
11 |
|
12 |
values[i] = NextValue(); |
13 |
}
|
14 |
|
15 |
ProcessItems(values); |
16 |
}
|
17 |
|
18 |
void ProcessItems(int[] values) |
19 |
{
|
20 |
// ... Process data.
|
21 |
}
|
This solution has several problems, but the most glaring is seen when more than 20 values are read. As the program is now, the values from 21 to n are simply ignored. This could be mitigated by allocating more than 20 values—perhaps 200 or 2000. Maybe the size could be configured by the user, or perhaps if the array became full a larger array could be allocated and all of the existing data copied into it. Ultimately these solutions create complexity and waste memory.
What we need is a collection that allows us to add an arbitrary number of integer values and then enumerate over those integers in the order that they were added. The collection should not have a fixed maximum size and random access indexing is not necessary. What we need is a linked list.
Before we go on and learn how the linked list data structure is designed and implemented, let’s preview what our ultimate solution might look like.
1 |
static void LoadItems() |
2 |
{
|
3 |
LinkedList list = new LinkedList(); |
4 |
while (true) |
5 |
{
|
6 |
int value = NextValue(); |
7 |
if (value != 0xFFFF) |
8 |
{
|
9 |
list.Add(value); |
10 |
}
|
11 |
else
|
12 |
{
|
13 |
break; |
14 |
}
|
15 |
}
|
16 |
|
17 |
ProcessItems(list); |
18 |
}
|
19 |
|
20 |
static void ProcessItems(LinkedList list) |
21 |
{
|
22 |
// ... Process data.
|
23 |
}
|
Notice that all of the problems with the array solution no longer exist. There are no longer any issues with the array not being large enough or allocating more than is necessary.
You should also notice that this solution informs some of the design decisions we will be making later, namely that the LinkedList class accepts a generic type argument and implements the IEnumerable interface.
Implementing a LinkedList Class
The Node
At the core of the linked list data structure is the Node class. A node is a container that provides the ability to both store data and connect to other nodes.
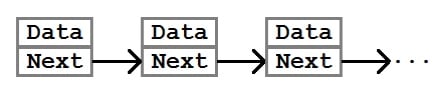


In its simplest form, a Node class that contains integers could look like this:
1 |
public class Node |
2 |
{
|
3 |
public int Value { get; set; } |
4 |
public Node Next { get; set; } |
5 |
}
|
With this we can now create a very primitive linked list. In the following example we will allocate three nodes (first, middle, and last) and then link them together into a list.
1 |
// +-----+------+ |
2 |
// | 3 | null + |
3 |
// +-----+------+ |
4 |
Node first = new Node { Value = 3 };
|
5 |
|
6 |
// +-----+------+ +-----+------+ |
7 |
// | 3 | null + | 5 | null + |
8 |
// +-----+------+ +-----+------+ |
9 |
Node middle = new Node { Value = 5 };
|
10 |
|
11 |
// +-----+------+ +-----+------+ |
12 |
// | 3 | *---+--->| 5 | null + |
13 |
// +-----+------+ +-----+------+ |
14 |
first.Next = middle; |
15 |
|
16 |
// +-----+------+ +-----+------+ +-----+------+ |
17 |
// | 3 | *---+--->| 5 | null + | 7 | null + |
18 |
// +-----+------+ +-----+------+ +-----+------+ |
19 |
Node last = new Node { Value = 7 };
|
20 |
|
21 |
// +-----+------+ +-----+------+ +-----+------+ |
22 |
// | 3 | *---+--->| 5 | *---+-->| 7 | null + |
23 |
// +-----+------+ +-----+------+ +-----+------+ |
24 |
middle.Next = last; |
We now have a linked list that starts with the node first and ends with the node last. The Next property for the last node points to null which is the end-of-list indicator. Given this list, we can perform some basic operations. For example, the value of each node’s Data property:
1 |
private static void PrintList(Node node) |
2 |
{
|
3 |
while (node != null) |
4 |
{
|
5 |
Console.WriteLine(node.Value); |
6 |
node = node.Next; |
7 |
}
|
8 |
}
|
The PrintList method works by iterating over each node in the list, printing the value of the current node, and then moving on to the node pointed to by the Next property.
Now that we have an understanding of what a linked list node might look like, let’s look at the actual LinkedListNode class.
1 |
public class LinkedListNode |
2 |
{
|
3 |
///
|
4 |
/// Constructs a new node with the specified value.
|
5 |
///
|
6 |
public LinkedListNode(T value) |
7 |
{
|
8 |
Value = value; |
9 |
}
|
10 |
|
11 |
///
|
12 |
/// The node value.
|
13 |
///
|
14 |
public T Value { get; internal set; } |
15 |
|
16 |
///
|
17 |
/// The next node in the linked list (null if last node).
|
18 |
///
|
19 |
public LinkedListNode Next { get; internal set; } |
20 |
}
|
The LinkedList Class
Before implementing our LinkedList class, we need to think about what we’d like to be able to do with the list.
Earlier we saw that the collection needs to support strongly typed data so we know we want to create a generic interface.
Since we’re using the .NET framework to implement the list, it makes sense that we would want this class to be able to act like the other built-in collection types. The easiest way to do this is to implement the ICollection<T> interface. Notice I choose ICollection<T> and not IList<T>. This is because the IList<T> interface adds the ability to access values by index. While direct indexing is generally useful, it cannot be efficiently implemented in a linked list.
With these requirements in mind we can create a basic class stub, and then through the rest of the section we can fill in these methods.
1 |
public class LinkedList : |
2 |
System.Collections.Generic.ICollection |
3 |
{
|
4 |
public void Add(T item) |
5 |
{
|
6 |
throw new System.NotImplementedException(); |
7 |
}
|
8 |
|
9 |
public void Clear() |
10 |
{
|
11 |
throw new System.NotImplementedException(); |
12 |
}
|
13 |
|
14 |
public bool Contains(T item) |
15 |
{
|
16 |
throw new System.NotImplementedException(); |
17 |
}
|
18 |
|
19 |
public void CopyTo(T[] array, int arrayIndex) |
20 |
{
|
21 |
throw new System.NotImplementedException(); |
22 |
}
|
23 |
|
24 |
public int Count |
25 |
{
|
26 |
get; |
27 |
private set; |
28 |
}
|
29 |
|
30 |
public bool IsReadOnly |
31 |
{
|
32 |
get { throw new System.NotImplementedException(); } |
33 |
}
|
34 |
|
35 |
public bool Remove(T item) |
36 |
{
|
37 |
throw new System.NotImplementedException(); |
38 |
}
|
39 |
|
40 |
public System.Collections.Generic.IEnumerator GetEnumerator() |
41 |
{
|
42 |
throw new System.NotImplementedException(); |
43 |
}
|
44 |
|
45 |
System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator() |
46 |
{
|
47 |
throw new System.NotImplementedException(); |
48 |
}
|
49 |
}
|
Add
| Behavior | Adds the provided value to the end of the linked list. |
| Performance | O(1) |
Adding an item to a linked list involves three steps:
- Allocate the new
LinkedListNodeinstance. - Find the last node of the existing list.
- Point the
Nextproperty of the last node to the new node.
The key is to know which node is the last node in the list. There are two ways we can know this. The first way is to keep track of the first node (the “head” node) and walk the list until we have found the last node. This approach does not require that we keep track of the last node, which saves one reference worth of memory (whatever your platform pointer size is), but does require that we perform a traversal of the list every time a node is added. This would make Add an O(n) operation.
The second approach requires that we keep track of the last node (the “tail” node) in the list and when we add the new node we simply access our stored reference directly. This is an O(1) algorithm and therefore the preferred approach.
The first thing we need to do is add two private fields to the LinkedList class: references to the first (head) and last (tail) nodes.
1 |
private LinkedListNode _head; |
2 |
private LinkedListNode _tail; |
Next we need to add the method that performs the three steps.
1 |
public void Add(T value) |
2 |
{
|
3 |
LinkedListNode node = new LinkedListNode(value); |
4 |
|
5 |
if (_head == null) |
6 |
{
|
7 |
_head = node; |
8 |
_tail = node; |
9 |
}
|
10 |
else
|
11 |
{
|
12 |
_tail.Next = node; |
13 |
_tail = node; |
14 |
}
|
15 |
|
16 |
Count++; |
17 |
}
|
First, it allocates the new LinkedListNode instance. Next, it checks whether the list is empty. If the list is empty, the new node is added simply by assigning the _head and _tail references to the new node. The new node is now both the first and last node in the list. If the list is not empty, the node is added to the end of the list and the _tail reference is updated to point to the new end of the list.
The Count property is incremented when a node is added to ensure the ICollection<T>. Count property returns the accurate value.
Remove
| Behavior | Removes the first node in the list whose value equals the provided value. The method returns true if a value was removed. Otherwise it returns false. |
| Performance | O(n) |
Before talking about the Remove algorithm, let’s take a look at what it is trying to accomplish. In the following figure, there are four nodes in a list. We want to remove the node with the value three.



When the removal is done, the list will be modified such that the Next property on the node with the value two points to the node with the value four.
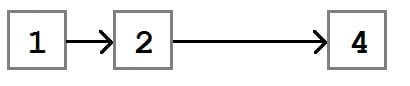

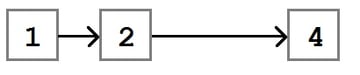
The basic algorithm for node removal is:
- Find the node to remove.
- Update the Next property of the node that precedes the node being removed to point to the node that follows the node being removed.
As always, the devil is in the details. There are a few cases we need to be thinking about when removing a node:
- The list might be empty, or the value we are trying to remove might not be in the list. In this case the list would remain unchanged.
- The node being removed might be the only node in the list. In this case we simply set the
_headand_tailfields tonull. - The node to remove might be the first node. In this case there is no preceding node, so instead we need to update the
_headfield to point to the new head node. - The node might be in the middle of the list.
- The node might be the last node in the list. In this case we update the
_tailfield to reference the penultimate node in the list and set itsNextproperty tonull.
1 |
public bool Remove(T item) |
2 |
{
|
3 |
LinkedListNode previous = null; |
4 |
LinkedListNode current = _head; |
5 |
|
6 |
// 1: Empty list: Do nothing.
|
7 |
// 2: Single node: Previous is null.
|
8 |
// 3: Many nodes:
|
9 |
// a: Node to remove is the first node.
|
10 |
// b: Node to remove is the middle or last.
|
11 |
|
12 |
while (current != null) |
13 |
{
|
14 |
if (current.Value.Equals(item)) |
15 |
{
|
16 |
// It's a node in the middle or end.
|
17 |
if (previous != null) |
18 |
{
|
19 |
// Case 3b.
|
20 |
|
21 |
// Before: Head -> 3 -> 5 -> null
|
22 |
// After: Head -> 3 ------> null
|
23 |
previous.Next = current.Next; |
24 |
|
25 |
// It was the end, so update _tail.
|
26 |
if (current.Next == null) |
27 |
{
|
28 |
_tail = previous; |
29 |
}
|
30 |
}
|
31 |
else
|
32 |
{
|
33 |
// Case 2 or 3a.
|
34 |
|
35 |
// Before: Head -> 3 -> 5
|
36 |
// After: Head ------> 5
|
37 |
|
38 |
// Head -> 3 -> null
|
39 |
// Head ------> null
|
40 |
_head = _head.Next; |
41 |
|
42 |
// Is the list now empty?
|
43 |
if (_head == null) |
44 |
{
|
45 |
_tail = null; |
46 |
}
|
47 |
}
|
48 |
|
49 |
Count--; |
50 |
|
51 |
return true; |
52 |
}
|
53 |
|
54 |
previous = current; |
55 |
current = current.Next; |
56 |
}
|
57 |
|
58 |
return false; |
59 |
}
|
The Count property is decremented when a node is removed to ensure the ICollection<T>. Count property returns the accurate value.
Contains
| Behavior | Returns a Boolean that indicates whether the provided value exists within the linked list. |
| Performance | O(n) |
The Contains method is quite simple. It looks at every node in the list, from first to last, and returns true as soon as a node matching the parameter is found. If the end of the list is reached and the node is not found, the method returns false.
1 |
public bool Contains(T item) |
2 |
{
|
3 |
LinkedListNode current = _head; |
4 |
while (current != null) |
5 |
{
|
6 |
if (current.Value.Equals(item)) |
7 |
{
|
8 |
return true; |
9 |
}
|
10 |
|
11 |
current = current.Next; |
12 |
}
|
13 |
|
14 |
return false; |
15 |
}
|
GetEnumerator
| Behavior | Returns an IEnumerator instance that allows enumerating the linked list values from first to last. |
| Performance | Returning the enumerator instance is an O(1) operation. Enumerating every item is an O(n) operation. |
GetEnumerator is implemented by enumerating the list from the first to last node and uses the C# yield keyword to return the current node’s value to the caller.
Notice that the LinkedList implements the iteration behavior in the IEnumerable<T> version of the GetEnumerator method and defers to this behavior in the IEnumerable version.
1 |
IEnumerator IEnumerable.GetEnumerator() |
2 |
{
|
3 |
LinkedListNode current = _head; |
4 |
while (current != null) |
5 |
{
|
6 |
yield return current.Value; |
7 |
current = current.Next; |
8 |
}
|
9 |
}
|
10 |
|
11 |
IEnumerator IEnumerable.GetEnumerator() |
12 |
{
|
13 |
return ((IEnumerable)this).GetEnumerator(); |
14 |
}
|
Clear
| Behavior | Removes all the items from the list. |
| Performance | O(1) |
The Clear method simply sets the _head and _tail fields to null to clear the list. Because .NET is a garbage collected language, the nodes do not need to be explicitly removed. It is the responsibility of the caller, not the linked list, to ensure that if the nodes contain IDisposable references they are properly disposed of.
1 |
public void Clear() |
2 |
{
|
3 |
_head = null; |
4 |
_tail = null; |
5 |
Count = 0; |
6 |
}
|
CopyTo
| Behavior | Copies the contents of the linked list from start to finish into the provided array, starting at the specified array index. |
| Performance | O(n) |
The CopyTo method simply iterates over the list items and uses simple assignment to copy the items to the array. It is the caller’s responsibility to ensure that the target array contains the appropriate free space to accommodate all the items in the list.
1 |
public void CopyTo(T[] array, int arrayIndex) |
2 |
{
|
3 |
LinkedListNode current = _head; |
4 |
while (current != null) |
5 |
{
|
6 |
array[arrayIndex++] = current.Value; |
7 |
current = current.Next; |
8 |
}
|
9 |
}
|
Count
| Behavior | Returns an integer indicating the number of items currently in the list. When the list is empty, the value returned is 0. |
| Performance | O(1) |
Count is simply an automatically implemented property with a public getter and private setter. The real behavior happens in the Add, Remove, and Clear methods.
1 |
public int Count |
2 |
{
|
3 |
get; |
4 |
private set; |
5 |
}
|
IsReadOnly
| Behavior | Returns false if the list is not read-only. |
| Performance | O(1) |
1 |
public bool IsReadOnly |
2 |
{
|
3 |
get { return false; } |
4 |
}
|
Doubly Linked List
The LinkedList class we just created is known as a singly, linked list. This means that there exists only a single, unidirectional link between a node and the next node in the list. There is a common variation of the linked list which allows the caller to access the list from both ends. This variation is known as a doubly linked list.
To create a doubly linked list we will need to first modify our LinkedListNode class to have a new property named Previous. Previous will act like Next, only it will point to the previous node in the list.



The following sections will only describe the changes between the singly linked list and the new doubly linked list.
Node Class
The only change that will be made in the LinkedListNode class is the addition of a new property named Previous which points to the previous LinkedListNode in the linked list, or returns null if it is the first node in the list.
1 |
public class LinkedListNode |
2 |
{
|
3 |
///
|
4 |
/// Constructs a new node with the specified value.
|
5 |
///
|
6 |
///
|
7 |
public LinkedListNode(T value) |
8 |
{
|
9 |
Value = value; |
10 |
}
|
11 |
|
12 |
///
|
13 |
/// The node value.
|
14 |
///
|
15 |
public T Value { get; internal set; } |
16 |
|
17 |
///
|
18 |
/// The next node in the linked list (null if last node).
|
19 |
///
|
20 |
public LinkedListNode Next { get; internal set; } |
21 |
|
22 |
///
|
23 |
/// The previous node in the linked list (null if first node).
|
24 |
///
|
25 |
public LinkedListNode Previous { get; internal set; } |
26 |
}
|
Add
While the singly linked list only added nodes to the end of the list, the doubly linked list will allow adding nodes to the start and end of the list using AddFirst and AddLast, respectively. The ICollection<T>. Add method will defer to the AddLast method to retain compatibility with the singly linked List class.
AddFirst
| Behavior | Adds the provided value to the front of the list. |
| Performance | O(1) |
When adding a node to the front of the list, the actions are very similar to adding to a singly linked list.
- Set the
Nextproperty of the new node to the old head node. - Set the
Previousproperty of the old head node to the new node. - Update the
_tailfield (if necessary) and incrementCount.
1 |
public void AddFirst(T value) |
2 |
{
|
3 |
LinkedListNode node = new LinkedListNode(value); |
4 |
|
5 |
// Save off the head node so we don't lose it.
|
6 |
LinkedListNode temp = _head; |
7 |
|
8 |
// Point head to the new node.
|
9 |
_head = node; |
10 |
|
11 |
// Insert the rest of the list behind head.
|
12 |
_head.Next = temp; |
13 |
|
14 |
if (Count == 0) |
15 |
{
|
16 |
// If the list was empty then head and tail should
|
17 |
// both point to the new node.
|
18 |
_tail = _head; |
19 |
}
|
20 |
else
|
21 |
{
|
22 |
// Before: head -------> 5 <-> 7 -> null
|
23 |
// After: head -> 3 <-> 5 <-> 7 -> null
|
24 |
temp.Previous = _head; |
25 |
}
|
26 |
|
27 |
Count++; |
28 |
}
|
AddLast
| Behavior | Adds the provided value to the end of the list. |
| Performance | O(1) |
Adding a node to the end of the list is even easier than adding one to the start.
The new node is simply appended to the end of the list, updating the state of _tail and _head as appropriate, and Count is incremented.
1 |
public void AddLast(T value) |
2 |
{
|
3 |
LinkedListNode node = new LinkedListNode(value); |
4 |
|
5 |
if (Count == 0) |
6 |
{
|
7 |
_head = node; |
8 |
}
|
9 |
else
|
10 |
{
|
11 |
_tail.Next = node; |
12 |
|
13 |
// Before: Head -> 3 <-> 5 -> null
|
14 |
// After: Head -> 3 <-> 5 <-> 7 -> null
|
15 |
// 7.Previous = 5
|
16 |
node.Previous = _tail; |
17 |
}
|
18 |
|
19 |
_tail = node; |
20 |
Count++; |
21 |
}
|
And as mentioned earlier, ICollection<T>.Add will now simply call AddLast.
1 |
public void Add(T value) |
2 |
{
|
3 |
AddLast(value); |
4 |
}
|
Remove
Like Add, the Remove method will be extended to support removing nodes from the start or end of the list. The ICollection<T>.Remove method will continue to remove items from the start with the only change being to update the appropriate Previous property.
RemoveFirst
| Behavior | Removes the first value from the list. If the list is empty, no action is taken. Returns true if a value was removed. Otherwise it returns false. |
| Performance | O(1) |
RemoveFirst updates the list by setting the linked list’s head property to the second node in the list and updating its Previous property to null. This removes all references to the previous head node, removing it from the list. If the list contained only a singleton, or was empty, the list will be empty (the head and tail properties will be null).
1 |
public void RemoveFirst() |
2 |
{
|
3 |
if (Count != 0) |
4 |
{
|
5 |
// Before: Head -> 3 <-> 5
|
6 |
// After: Head -------> 5
|
7 |
|
8 |
// Head -> 3 -> null
|
9 |
// Head ------> null
|
10 |
_head = _head.Next; |
11 |
|
12 |
Count--; |
13 |
|
14 |
if (Count == 0) |
15 |
{
|
16 |
_tail = null; |
17 |
}
|
18 |
else
|
19 |
{
|
20 |
// 5.Previous was 3; now it is null.
|
21 |
_head.Previous = null; |
22 |
}
|
23 |
}
|
24 |
}
|
RemoveLast
| Behavior | Removes the last node from the list. If the list is empty, no action is performed. Returns true if a value was removed. Otherwise, it returns false. |
| Performance | O(1) |
RemoveLast works by setting the list's tail property to be the node preceding the current tail node. This removes the last node from the list. If the list was empty or had only one node, when the method returns the head and tail properties, they will both be null.
1 |
public void RemoveLast() |
2 |
{
|
3 |
if (Count != 0) |
4 |
{
|
5 |
if (Count == 1) |
6 |
{
|
7 |
_head = null; |
8 |
_tail = null; |
9 |
}
|
10 |
else
|
11 |
{
|
12 |
// Before: Head --> 3 --> 5 --> 7
|
13 |
// Tail = 7
|
14 |
// After: Head --> 3 --> 5 --> null
|
15 |
// Tail = 5
|
16 |
// Null out 5's Next property.
|
17 |
_tail.Previous.Next = null; |
18 |
_tail = _tail.Previous; |
19 |
}
|
20 |
|
21 |
Count--; |
22 |
}
|
23 |
}
|
Remove
| Behavior | Removes the first node in the list whose value equals the provided value. The method returns true if a value was removed. Otherwise it returns false. |
| Performance | O(n) |
The ICollection<T>. Remove method is nearly identical to the singly linked version except that the Previous property is now updated during the remove operation. To avoid repeated code, the method calls RemoveFirst when it is determined that the node being removed is the first node in the list.
1 |
public bool Remove(T item) |
2 |
{
|
3 |
LinkedListNode previous = null; |
4 |
LinkedListNode current = _head; |
5 |
|
6 |
// 1: Empty list: Do nothing.
|
7 |
// 2: Single node: Previous is null.
|
8 |
// 3: Many nodes:
|
9 |
// a: Node to remove is the first node.
|
10 |
// b: Node to remove is the middle or last.
|
11 |
|
12 |
while (current != null) |
13 |
{
|
14 |
// Head -> 3 -> 5 -> 7 -> null
|
15 |
// Head -> 3 ------> 7 -> null
|
16 |
if (current.Value.Equals(item)) |
17 |
{
|
18 |
// It's a node in the middle or end.
|
19 |
if (previous != null) |
20 |
{
|
21 |
// Case 3b.
|
22 |
previous.Next = current.Next; |
23 |
|
24 |
// It was the end, so update _tail.
|
25 |
if (current.Next == null) |
26 |
{
|
27 |
_tail = previous; |
28 |
}
|
29 |
else
|
30 |
{
|
31 |
// Before: Head -> 3 <-> 5 <-> 7 -> null
|
32 |
// After: Head -> 3 <-------> 7 -> null
|
33 |
|
34 |
// previous = 3
|
35 |
// current = 5
|
36 |
// current.Next = 7
|
37 |
// So... 7.Previous = 3
|
38 |
current.Next.Previous = previous; |
39 |
}
|
40 |
|
41 |
Count--; |
42 |
}
|
43 |
else
|
44 |
{
|
45 |
// Case 2 or 3a.
|
46 |
RemoveFirst(); |
47 |
}
|
48 |
|
49 |
return true; |
50 |
}
|
51 |
|
52 |
previous = current; |
53 |
current = current.Next; |
54 |
}
|
55 |
|
56 |
return false; |
57 |
}
|
But Why?
We can add nodes to the front and end of the list—so what? Why do we care? As it stands right now, the doubly linked List class is no more powerful than the singly linked list. But with just one minor modification, we can open up all kinds of possible behaviors. By exposing the head and tail properties as read-only public properties, the linked list consumer will be able to implement all sorts of new behaviors.
1 |
public LinkedListNode Head |
2 |
{
|
3 |
get
|
4 |
{
|
5 |
return _head; |
6 |
}
|
7 |
}
|
8 |
|
9 |
public LinkedListNode Tail |
10 |
{
|
11 |
get
|
12 |
{
|
13 |
return _tail; |
14 |
}
|
15 |
}
|
With this simple change we can enumerate the list manually, which allows us to perform reverse (tail-to-head) enumeration and search.
For example, the following code sample shows how to use the list's Tail and Previous properties to enumerate the list in reverse and perform some processing on each node.
1 |
public void ProcessListBackwards() |
2 |
{
|
3 |
LinkedList list = new LinkedList(); |
4 |
PopulateList(list); |
5 |
|
6 |
LinkedListNode current = list.Tail; |
7 |
while (current != null) |
8 |
{
|
9 |
ProcessNode(current); |
10 |
current = current.Previous; |
11 |
}
|
12 |
}
|
Additionally, the doubly linked List class allows us to easily create the Deque class, which is itself a building block for other classes. We will discuss this class later in another section.
Next Up
This completes the second part about linked lists. Next up, we'll move on to the array list.












