El árbol de búsqueda binaria
Spanish (Español) translation by CYC (you can also view the original English article)
Listas enlazadas contienen datos de un nodo partido a un solo nodo de terminación. Listas enlazadas contienen datos de un nodo partido a un solo nodo de terminación. Arreglos de discos de contienen datos en bloques contiguos, unidimensionales.
Resumen
En esta sección, veremos cómo añadir una dimensión más nos permitirá introducir una nueva estructura de datos: el árbol. Específicamente, buscará un tipo de árbol conocido como árbol de búsqueda binaria. Árboles de búsqueda binaria tiene la estructura general del árbol y aplicarán un conjunto de reglas simples que definen la estructura del árbol.
Vamos a aprender antes de aprender acerca de esas reglas, qué árbol es.
Resumen de árbol
Un árbol es una estructura de datos donde cada nodo tiene cero o más hijos. Por ejemplo, podríamos tener un árbol como este:
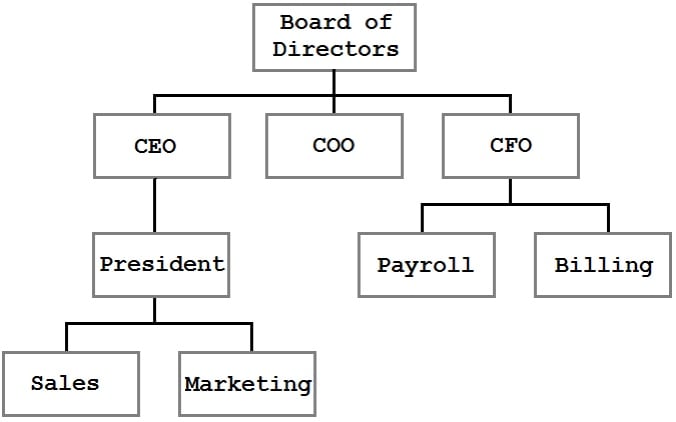
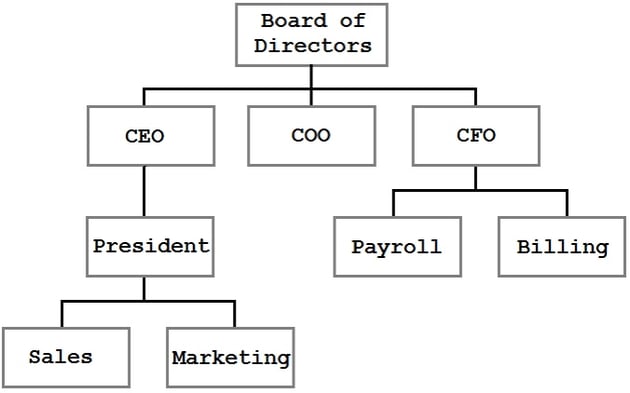
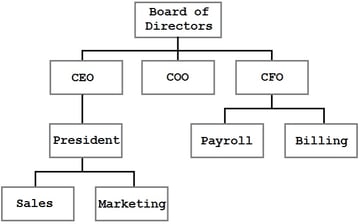
En este árbol, podemos ver la estructura organizacional de una empresa. Los bloques representan personas o divisiones dentro de la empresa y la líneas representan informes relaciones. Un árbol es una forma muy eficiente, lógica para presentar y almacenar esta información.
The tree shown in the previous figure is a general tree. It represents parent/child relationships, but there are no rules for the structure. El árbol que se muestra en la figura anterior es un árbol general.El CEO tiene un informe directo, pero podría fácilmente tener veinte o ninguno. En la figura, Sales (ventas) se muestra a la izquierda de Marketing, pero ese orden no tiene ningún significado. De hecho, la única restricción observable es que cada nodo tiene como máximo un padre (y el nodo superior, el Consejo de Administración, no tiene padre).
Descripción del árbol de búsqueda binaria
Un árbol de búsqueda binaria utiliza la misma estructura básica que el árbol general que se muestra en la última figura, pero con la adición de algunas reglas. Estas reglas son:
- Cada nodo puede tener cero, uno o dos hijos.
- Cualquier valor menor que el valor del nodo va al hijo de la izquierda (o un hijo del hijo de la izquierda).
- Cualquier valor mayor que, o igual a, el valor del nodo va al hijo correcto (o un hijo de eso).
Miremos un árbol que se construye usando estas reglas:

Observa cómo las restricciones que especificamos se aplican en el diagrama. Cada valor a la izquierda del nodo raíz (ocho) tiene un valor menor que ocho, y cada valor a la derecha es mayor o igual que el nodo raíz. Esta regla se aplica recursivamente en cada nodo en el camino.
Con este árbol en mente, pensemos en los pasos que se dieron para construirlo. Cuando comenzó el proceso, el árbol estaba vacío y luego se agregó un valor de ocho. Debido a que fue el primer valor agregado, se colocó en la posición raíz (último padre).
No sabemos el orden exacto en que se agregaron el resto de los nodos, pero voy a presentar una ruta posible. Los valores se agregarán usando un método llamado Add que acepta el valor.
1 |
BinaryTree tree = new BinaryTree(); |
2 |
tree.Add(8); |
3 |
tree.Add(4); |
4 |
tree.Add(2); |
5 |
tree.Add(3); |
6 |
tree.Add(10); |
7 |
tree.Add(6); |
8 |
tree.Add(7); |
Veamos los primeros artículos.
Ocho fue agregado primero y se convirtió en la raíz. Luego, se agregó el cuatro. Como cuatro es menor que ocho, debe ir a la izquierda de ocho según la regla número dos. Como ocho no tienen ningún hijo a la izquierda, cuatro se convierte en el hijo izquierdo inmediato de ocho.
Dos se agrega a continuación. Dos es menor que ocho, por lo que va a la izquierda. Ya hay un nodo a la izquierda de ocho, por lo que la lógica de comparación se realiza nuevamente. Dos es menor que cuatro y cuatro no tienen ningún hijo izquierdo, por lo que dos se convierten en el hijo izquierdo de cuatro.
Tres se agrega a continuación y va a la izquierda de ocho y cuatro. Cuando se compara con los dos nodos, es más grande, por lo que se agrega tres a la derecha de dos según la regla número tres.
Este ciclo de comparación de valores en cada nodo y después de verificar cada hijo una y otra vez hasta encontrar el espacio adecuado se repite para cada valor hasta que se crea la estructura final del árbol.
La clase Nodo
BinaryTreeNode representa un solo nodo en el árbol. Contiene referencias a los secundarios izquierdo y derecho (nulo si no hay ninguno), el valor del nodo y el método IComparable.CompareTo que permite comparar los valores del nodo para determinar si el valor debe ir a la izquierda o a la derecha del nodo actual. Esta es toda la clase BinaryTreeNode; como puedes ver, es muy simple.
1 |
class BinaryTreeNode : IComparable |
2 |
where TNode : IComparable |
3 |
{
|
4 |
public BinaryTreeNode(TNode value) |
5 |
{
|
6 |
Value = value; |
7 |
}
|
8 |
|
9 |
public BinaryTreeNode Left { get; set; } |
10 |
public BinaryTreeNode Right { get; set; } |
11 |
public TNode Value { get; private set; } |
12 |
|
13 |
///
|
14 |
/// Compares the current node to the provided value.
|
15 |
///
|
16 |
/// The node value to compare to
|
17 |
/// 1 if the instance value is greater than
|
18 |
/// the provided value, -1 if less, or 0 if equal.
|
19 |
public int CompareTo(TNode other) |
20 |
{
|
21 |
return Value.CompareTo(other); |
22 |
}
|
23 |
}
|
La clase Árbol de búsqueda binaria
La clase BinaryTree proporciona los métodos básicos que necesitas para manipular el árbol: Add, Remove, un método Contains para determinar si un elemento existe en el árbol, varios métodos de cruce y enumeración (estos son métodos que nos permiten enumerar los nodos en el árbol en varios órdenes bien definidos) y los métodos normales count y clear.
Para inicializar el árbol, hay una referencia BinaryTreeNode que representa el nodo principal (raíz) del árbol, y hay un número entero que realiza un seguimiento de cuántos elementos hay en el árbol.
1 |
public class BinaryTree : IEnumerable |
2 |
where T : IComparable |
3 |
{
|
4 |
private BinaryTreeNode _head; |
5 |
private int _count; |
6 |
|
7 |
public void Add(T value) |
8 |
{
|
9 |
throw new NotImplementedException(); |
10 |
}
|
11 |
|
12 |
public bool Contains(T value) |
13 |
{
|
14 |
throw new NotImplementedException(); |
15 |
}
|
16 |
|
17 |
public bool Remove(T value) |
18 |
{
|
19 |
throw new NotImplementedException(); |
20 |
}
|
21 |
|
22 |
public void PreOrderTraversal(Action action) |
23 |
{
|
24 |
throw new NotImplementedException(); |
25 |
}
|
26 |
|
27 |
public void PostOrderTraversal(Action action) |
28 |
{
|
29 |
throw new NotImplementedException(); |
30 |
}
|
31 |
|
32 |
public void InOrderTraversal(Action action) |
33 |
{
|
34 |
throw new NotImplementedException(); |
35 |
}
|
36 |
|
37 |
public IEnumerator GetEnumerator() |
38 |
{
|
39 |
throw new NotImplementedException(); |
40 |
}
|
41 |
|
42 |
System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator() |
43 |
{
|
44 |
throw new NotImplementedException(); |
45 |
}
|
46 |
|
47 |
public void Clear() |
48 |
{
|
49 |
throw new NotImplementedException(); |
50 |
}
|
51 |
|
52 |
public int Count |
53 |
{
|
54 |
get; |
55 |
}
|
56 |
}
|
Add
| Comportamiento | Agrega el valor provisto a la ubicación correcta dentro del árbol. |
| Rendimiento | O(log n) en promedio; O(n) en el peor de los casos. |
Agregar un nodo al árbol no es terriblemente complejo y se hace aún más fácil cuando el problema se simplifica en un algoritmo recursivo. Hay dos casos que deben considerarse:
- Cuando el árbol está vacío.
- Cuando el árbol no está vacío.
En el primer caso, simplemente asignamos el nuevo nodo y lo agregamos al árbol. En el segundo caso, comparamos el valor con el valor del nodo. Si el valor que intentamos agregar es menor que el valor del nodo, el algoritmo se repite para el elemento secundario izquierdo del nodo. De lo contrario, se repite para el hijo derecho del nodo.
1 |
public void Add(T value) |
2 |
{
|
3 |
// Case 1: The tree is empty. Allocate the head.
|
4 |
if (_head == null) |
5 |
{
|
6 |
_head = new BinaryTreeNode(value); |
7 |
}
|
8 |
// Case 2: The tree is not empty, so recursively
|
9 |
// find the right location to insert the node.
|
10 |
else
|
11 |
{
|
12 |
AddTo(_head, value); |
13 |
}
|
14 |
|
15 |
_count++; |
16 |
}
|
17 |
|
18 |
// Recursive add algorithm.
|
19 |
private void AddTo(BinaryTreeNode node, T value) |
20 |
{
|
21 |
// Case 1: Value is less than the current node value
|
22 |
if (value.CompareTo(node.Value) < 0) |
23 |
{
|
24 |
// If there is no left child, make this the new left,
|
25 |
if (node.Left == null) |
26 |
{
|
27 |
node.Left = new BinaryTreeNode(value); |
28 |
}
|
29 |
else
|
30 |
{
|
31 |
// else add it to the left node.
|
32 |
AddTo(node.Left, value); |
33 |
}
|
34 |
}
|
35 |
// Case 2: Value is equal to or greater than the current value.
|
36 |
else
|
37 |
{
|
38 |
// If there is no right, add it to the right,
|
39 |
if (node.Right == null) |
40 |
{
|
41 |
node.Right = new BinaryTreeNode(value); |
42 |
}
|
43 |
else
|
44 |
{
|
45 |
// else add it to the right node.
|
46 |
AddTo(node.Right, value); |
47 |
}
|
48 |
}
|
49 |
}
|
Remove
| Comportamiento | Elimina el primer nombre encontrado con el valor indicado. |
| Rendimiento | O(log n) en promedio; O(n) en el peor de los casos. |
Eliminar un valor del árbol es una operación conceptualmente simple que se vuelve sorprendentemente compleja en la práctica.
En un nivel alto, la operación es simple:
- Encontrar el nodo para eliminar
- Eliminarlo
El primer paso es simple, y como veremos, se logra utilizando el mismo mecanismo que usa el método Contains. Sin embargo, una vez que se identifica el nodo que se va a eliminar, la operación puede tomar una de las tres rutas dictadas por el estado del árbol alrededor del nodo que se va a eliminar. Los tres estados se describen en los siguientes tres casos.
Caso uno: El nodo que se eliminará no tiene ningún hijo a la derecha.

En este caso, la operación de eliminación simplemente puede mover el elemento secundario izquierdo, si hay uno, al lugar del nodo eliminado. El árbol resultante se vería así:

Caso dos: El nodo que se eliminará tiene un hijo derecho que, a su vez, no tiene ningún hijo izquierdo.

En este caso, queremos mover el hijo derecho (seis) del nodo eliminado al lugar del nodo eliminado. El árbol resultante se verá así:

Caso tres: El nodo que se eliminará tiene un hijo derecho que, a su vez, tiene un hijo izquierdo.

En este caso, el hijo que está en la la izquierda del hijo derecho del nodo eliminado debe colocarse en el espacio del nodo eliminado.
Tomemos un minuto para pensar por qué esto es cierto. Hay dos hechos que sabemos sobre el subárbol comenzando con el nodo que se elimina (por ejemplo, el subárbol cuya raíz es el nodo con el valor cinco).
- Cada valor a la derecha del nodo es mayor o igual a cinco.
- El valor más pequeño en el subárbol correcto es el nodo situado más a la izquierda.
Necesitamos colocar un valor en la ranura del nodo eliminado que es más pequeño que, o igual a, cada nodo a su derecha. Para hacer eso, necesitamos obtener el valor más pequeño en el lado derecho. Por lo tanto, necesitamos el nodo izquierdo de la derecha del hijo.
Después de la eliminación del nodo, el árbol se verá así:

Ahora que entendemos los tres escenarios eliminados, veamos el código para hacerlo realidad.
Una cosa a tener en cuenta: el método FindWithParent (consulta la sección Contains) devuelve el nodo para eliminar así como también el padre del nodo que se está eliminando. Esto se hace porque cuando se elimina el nodo, tenemos que actualizar la propiedad left o right de los padres para apuntar al nuevo nodo.
Podríamos evitar hacer esto si todos los nodos mantuvieran una referencia a su padre, pero eso introduciría una sobrecarga de memoria por nodo y costos de contabilidad que solo son necesarios en este caso.
1 |
public bool Remove(T value) |
2 |
{
|
3 |
BinaryTreeNode current, parent; |
4 |
|
5 |
// Find the node to remove.
|
6 |
current = FindWithParent(value, out parent); |
7 |
|
8 |
if (current == null) |
9 |
{
|
10 |
return false; |
11 |
}
|
12 |
|
13 |
_count--; |
14 |
|
15 |
// Case 1: If current has no right child, current's left replaces current.
|
16 |
if (current.Right == null) |
17 |
{
|
18 |
if (parent == null) |
19 |
{
|
20 |
_head = current.Left; |
21 |
}
|
22 |
else
|
23 |
{
|
24 |
int result = parent.CompareTo(current.Value); |
25 |
if (result > 0) |
26 |
{
|
27 |
// If parent value is greater than current value,
|
28 |
// make the current left child a left child of parent.
|
29 |
parent.Left = current.Left; |
30 |
}
|
31 |
else if (result < 0) |
32 |
{
|
33 |
// If parent value is less than current value,
|
34 |
// make the current left child a right child of parent.
|
35 |
parent.Right = current.Left; |
36 |
}
|
37 |
}
|
38 |
}
|
39 |
// Case 2: If current's right child has no left child, current's right child
|
40 |
// replaces current.
|
41 |
else if (current.Right.Left == null) |
42 |
{
|
43 |
current.Right.Left = current.Left; |
44 |
|
45 |
if (parent == null) |
46 |
{
|
47 |
_head = current.Right; |
48 |
}
|
49 |
else
|
50 |
{
|
51 |
int result = parent.CompareTo(current.Value); |
52 |
if (result > 0) |
53 |
{
|
54 |
// If parent value is greater than current value,
|
55 |
// make the current right child a left child of parent.
|
56 |
parent.Left = current.Right; |
57 |
}
|
58 |
else if (result < 0) |
59 |
{
|
60 |
// If parent value is less than current value,
|
61 |
// make the current right child a right child of parent.
|
62 |
parent.Right = current.Right; |
63 |
}
|
64 |
}
|
65 |
}
|
66 |
// Case 3: If current's right child has a left child, replace current with current's
|
67 |
// right child's left-most child.
|
68 |
else
|
69 |
{
|
70 |
// Find the right's left-most child.
|
71 |
BinaryTreeNode leftmost = current.Right.Left; |
72 |
BinaryTreeNode leftmostParent = current.Right; |
73 |
|
74 |
while (leftmost.Left != null) |
75 |
{
|
76 |
leftmostParent = leftmost; |
77 |
leftmost = leftmost.Left; |
78 |
}
|
79 |
|
80 |
// The parent's left subtree becomes the leftmost's right subtree.
|
81 |
leftmostParent.Left = leftmost.Right; |
82 |
|
83 |
// Assign leftmost's left and right to current's left and right children.
|
84 |
leftmost.Left = current.Left; |
85 |
leftmost.Right = current.Right; |
86 |
|
87 |
if (parent == null) |
88 |
{
|
89 |
_head = leftmost; |
90 |
}
|
91 |
else
|
92 |
{
|
93 |
int result = parent.CompareTo(current.Value); |
94 |
if (result > 0) |
95 |
{
|
96 |
// If parent value is greater than current value,
|
97 |
// make leftmost the parent's left child.
|
98 |
parent.Left = leftmost; |
99 |
}
|
100 |
else if (result < 0) |
101 |
{
|
102 |
// If parent value is less than current value,
|
103 |
// make leftmost the parent's right child.
|
104 |
parent.Right = leftmost; |
105 |
}
|
106 |
}
|
107 |
}
|
108 |
|
109 |
return true; |
110 |
}
|
<!--td {border: 1px solid #ccc;}br {mso-data-placement:same-cell;}-->Contains
| Comportamiento | Devuelve verdadero si el árbol contiene el valor proporcionado. De lo contrario, devuelve falso. |
| Rendimiento | O(log n) en promedio; O(n) en el peor de los casos. |
Contains difiere a FindWithParent, que realiza un algoritmo simple de caminar en árbol que realiza los siguientes pasos, comenzando en el nodo principal:
- Si el nodo actual es nulo, devuelve nulo.
- Si el valor del nodo actual es igual al valor buscado, devuelva el nodo actual.
- Si el valor buscado es menor que el valor actual, configura el nodo actual como hijo izquierdo y va al paso número uno.
- Establece el nodo actual en el secundario derecho y va al paso número uno.
Dado que Contains devuelve un valor booleano, el valor devuelto se determina según si FindWithParent devuelve un BinaryTreeNode (true) no nulo o uno nulo (falso).
El método Remove también lo utiliza el método FindWithParent. El parámetro out, parent, no es utilizado por Contains.
1 |
public bool Contains(T value) |
2 |
{
|
3 |
// Defer to the node search helper function.
|
4 |
BinaryTreeNode parent; |
5 |
return FindWithParent(value, out parent) != null; |
6 |
}
|
7 |
|
8 |
///
|
9 |
/// Finds and returns the first node containing the specified value. If the value
|
10 |
/// is not found, it returns null. Also returns the parent of the found node (or null)
|
11 |
/// which is used in Remove.
|
12 |
///
|
13 |
private BinaryTreeNode FindWithParent(T value, out BinaryTreeNode parent) |
14 |
{
|
15 |
// Now, try to find data in the tree.
|
16 |
BinaryTreeNode current = _head; |
17 |
parent = null; |
18 |
|
19 |
// While we don't have a match...
|
20 |
while (current != null) |
21 |
{
|
22 |
int result = current.CompareTo(value); |
23 |
|
24 |
if (result > 0) |
25 |
{
|
26 |
// If the value is less than current, go left.
|
27 |
parent = current; |
28 |
current = current.Left; |
29 |
}
|
30 |
else if (result < 0) |
31 |
{
|
32 |
// If the value is more than current, go right.
|
33 |
parent = current; |
34 |
current = current.Right; |
35 |
}
|
36 |
else
|
37 |
{
|
38 |
// We have a match!
|
39 |
break; |
40 |
}
|
41 |
}
|
42 |
|
43 |
return current; |
44 |
}
|
Count
| Comportamiento | Devuelve el número de valores en el árbol (0 si está vacío). |
| Rendimiento | O(1) |
El campo de recuento se incrementa mediante el método Add y se disminuye mediante el método Remove.
1 |
public int Count |
2 |
{
|
3 |
get
|
4 |
{
|
5 |
return _count; |
6 |
}
|
7 |
}
|
Clear
| Comportamiento | Elimina todos los nodos del árbol. |
| Rendimiento | O(1) |
1 |
public void Clear() |
2 |
{
|
3 |
_head = null; |
4 |
_count = 0; |
5 |
}
|
Traversals
Los recorridos de árbol son algoritmos que permiten procesar cada valor en el árbol en un orden bien definido. Para cada uno de los algoritmos discutidos, se utilizará el siguiente árbol como entrada de muestra.
Los ejemplos que siguen a todos aceptan un parámetro Action<T>. Este parámetro define la acción que se aplicará a cada nodo a medida que sea procesado por el recorrido.
La sección Order para cada cruce indicará el orden en que se moverá el siguiente árbol.

Preorder
| Comportamiento | Realiza la acción provista en cada valor en preorden (mira la descripción que sigue). |
| Rendimiento | O(n) |
| Orden | 4, 2, 1, 3, 5, 7, 6, 8 |
El recorrido de preorden procesa el nodo actual antes de pasar a los secundarios izquierdo y derecho. Comenzando en el nodo raíz, cuatro, la acción se ejecuta con el valor cuatro. Luego se procesa el nodo izquierdo y todos sus elementos secundarios, seguidos por el nodo derecho y todos sus elementos secundarios.
Un uso común del recorrido de preorden sería crear una copia del árbol que contenga no solo los mismos valores de nodo, sino también la misma jerarquía.
1 |
public void PreOrderTraversal(Action action) |
2 |
{
|
3 |
PreOrderTraversal(action, _head); |
4 |
}
|
5 |
|
6 |
private void PreOrderTraversal(Action action, BinaryTreeNode node) |
7 |
{
|
8 |
if (node != null) |
9 |
{
|
10 |
action(node.Value); |
11 |
PreOrderTraversal(action, node.Left); |
12 |
PreOrderTraversal(action, node.Right); |
13 |
}
|
14 |
}
|
Postorder
| Comportamiento | Realiza la acción proporcionada en cada valor en postorder (ver la descripción que sigue). |
| Rendimiento | O(n) |
| Orden | <!--td {border: 1px solid #ccc;}br {mso-data-placement:same-cell;}-->1, 3, 2, 6, 8, 7, 5, 4 |
El recorrido del postorder visita el elemento secundario derecho e izquierdo del nodo de forma recursiva, y luego realiza la acción en el nodo actual una vez que los elementos secundarios están completos.
Los recorridos posteriores al pedido a menudo se utilizan para eliminar un árbol completo, como en los lenguajes de programación donde debe liberarse cada nodo o para eliminar subárboles. Este es el caso porque el nodo raíz se procesa (elimina) al último y sus hijos se procesan de una manera que minimice la cantidad de trabajo que el algoritmo Remove necesita realizar.
1 |
public void PostOrderTraversal(Action action) |
2 |
{
|
3 |
PostOrderTraversal(action, _head); |
4 |
}
|
5 |
|
6 |
private void PostOrderTraversal(Action action, BinaryTreeNode node) |
7 |
{
|
8 |
if (node != null) |
9 |
{
|
10 |
PostOrderTraversal(action, node.Left); |
11 |
PostOrderTraversal(action, node.Right); |
12 |
action(node.Value); |
13 |
}
|
14 |
}
|
Inorder
| Comportamiento | Realiza la acción proporcionada en cada valor en orden. (Ver la descripción que sigue). |
| Rendimiento | O(n) |
| Orden | 1, 2, 3, 4, 5, 6, 7, 8 |
Inorder transversal procesa los nodos en el orden de clasificación: en el ejemplo anterior, los nodos se ordenarían en orden numérico, del más pequeño al más grande. Para ello, busca el nodo más pequeño (más a la izquierda) y luego lo procesa antes de procesar los nodos más grandes (a la derecha).
Los recorridos de Inorder senodos deben pro utilizan cada vez que los cesarse en orden de clasificación.
El ejemplo que sigue muestra dos métodos diferentes para realizar un recorrido de tipo inorden. El primero implementa un enfoque recursivo que realiza una devolución de llamada para cada nodo atravesado. El segundo elimina la recursión mediante el uso de la estructura de datos de pila y devuelve un IEnumerator para permitir la enumeración directa.
1 |
Public void InOrderTraversal(Action action) |
2 |
{
|
3 |
InOrderTraversal(action, _head); |
4 |
}
|
5 |
|
6 |
private void InOrderTraversal(Action action, BinaryTreeNode node) |
7 |
{
|
8 |
if (node != null) |
9 |
{
|
10 |
InOrderTraversal(action, node.Left); |
11 |
|
12 |
action(node.Value); |
13 |
|
14 |
InOrderTraversal(action, node.Right); |
15 |
}
|
16 |
}
|
17 |
|
18 |
public IEnumerator InOrderTraversal() |
19 |
{
|
20 |
// This is a non-recursive algorithm using a stack to demonstrate removing
|
21 |
// recursion.
|
22 |
if (_head != null) |
23 |
{
|
24 |
// Store the nodes we've skipped in this stack (avoids recursion).
|
25 |
Stack> stack = new Stack>(); |
26 |
|
27 |
BinaryTreeNode current = _head; |
28 |
|
29 |
// When removing recursion, we need to keep track of whether
|
30 |
// we should be going to the left node or the right nodes next.
|
31 |
bool goLeftNext = true; |
32 |
|
33 |
// Start by pushing Head onto the stack.
|
34 |
stack.Push(current); |
35 |
|
36 |
while (stack.Count > 0) |
37 |
{
|
38 |
// If we're heading left...
|
39 |
if (goLeftNext) |
40 |
{
|
41 |
// Push everything but the left-most node to the stack.
|
42 |
// We'll yield the left-most after this block.
|
43 |
while (current.Left != null) |
44 |
{
|
45 |
stack.Push(current); |
46 |
current = current.Left; |
47 |
}
|
48 |
}
|
49 |
|
50 |
// Inorder is left->yield->right.
|
51 |
yield return current.Value; |
52 |
|
53 |
// If we can go right, do so.
|
54 |
if (current.Right != null) |
55 |
{
|
56 |
current = current.Right; |
57 |
|
58 |
// Once we've gone right once, we need to start
|
59 |
// going left again.
|
60 |
goLeftNext = true; |
61 |
}
|
62 |
else
|
63 |
{
|
64 |
// If we can't go right, then we need to pop off the parent node
|
65 |
// so we can process it and then go to its right node.
|
66 |
current = stack.Pop(); |
67 |
goLeftNext = false; |
68 |
}
|
69 |
}
|
70 |
}
|
71 |
}
|
GetEnumerator
| Comportamiento | Devuelve un enumerador utilizando el algoritmo de recorrido InOrder. |
| Rendimiento | O(1) para devolver el enumerador. La enumeración de todos los elementos es O(n). |
1 |
public IEnumerator GetEnumerator() |
2 |
{
|
3 |
return InOrderTraversal(); |
4 |
}
|
5 |
|
6 |
System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator() |
7 |
{
|
8 |
return GetEnumerator(); |
9 |
}
|












