The Binary Search Algorithm in JavaScript

In this post, I'll compare linear search and binary search algorithms. You'll learn pseudocode for linear and binary algorithms, see examples to demonstrate both the methods, learn about time complexity, and get a step-by-step guide on how to implement the algorithms.
Introduction
As a programmer, you want to find the best solution to a problem so that your code is not only correct but also efficient. Choosing a suboptimal algorithm could mean a longer completion time, increased code complexity, or worse, a program that crashes.
You may have used a search algorithm to locate items in a collection of data. The JavaScript language has several methods, like find, to locate items in an array. However, these methods use linear search. A linear search algorithm starts at the beginning of a list and compares each element with the search value until it is found.
This is fine when you have a small number of elements. But when you are searching large lists that have thousands or millions of elements, you need a better way to locate items. This is when you would use binary search.
In this tutorial, I will explain how binary search works and how to implement the algorithm in JavaScript. First, we will review the linear search algorithm.
Linear Search
We will begin by explaining how to implement linear search in JavaScript. We will create a function called linearSearch that accepts a value that is an integer or string and an array as parameters. The function will search every element in the array for the value and return the position of the value in the array if it is found. If the value is not in the array, it will return -1.
Pseudocode for Linear Search
1 |
Set found to false |
2 |
Set position to −1 |
3 |
Set index to 0 |
4 |
while found is false and index < number of elements |
5 |
if list[index] is equal to search value |
6 |
Set found to true |
7 |
Set position to index |
8 |
else Add 1 to index |
9 |
return position |
Step-by-Step Explanation of Linear Search
Imagine our input to the linear search is [1,9,13,16,3,4,0,12]. If the value we're searching for is 16, the above logic would return 3. And, if we search for 11, the above logic will return -1. Let's break it down.
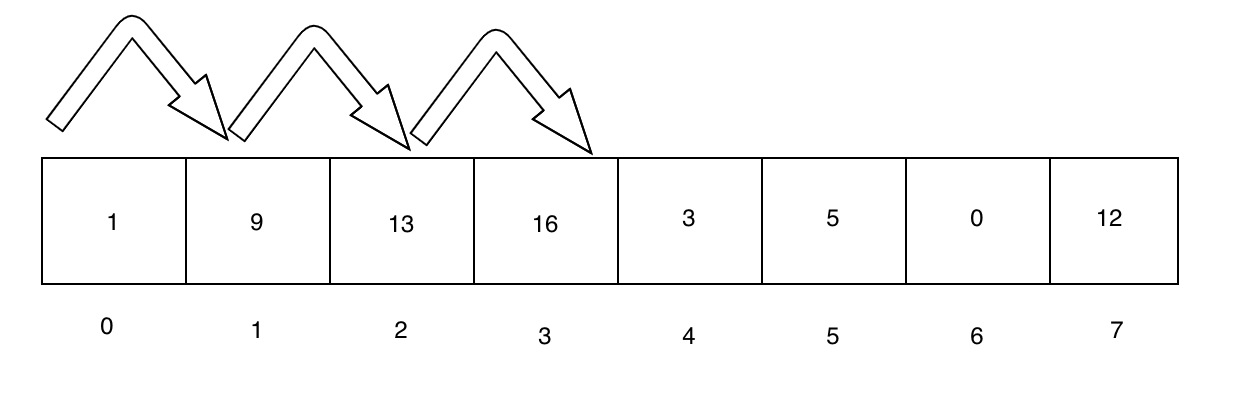
We initialise the algorithm by setting found to false, position to -1, and index to 0. Then we iterate:
| Step | index |
list[index] |
position |
found |
|---|---|---|---|---|
| 1 | 0 |
1 |
-1 |
false |
| 2 | 1 |
9 |
-1 |
false |
| 3 | 2 |
13 |
-1 |
false |
| 4 | 3 |
16 |
3 |
true |
If we follow the above logic for an element that is not present in the array, you'll see the code returning -1, since found = false, and position = -1 till the end.
Javascript Implementation of Linear Search
Here is a JavaScript implementation of the linear search algorithm:
1 |
function linearSearch(value, list) { |
2 |
let found = false; |
3 |
let position = -1; |
4 |
let index = 0; |
5 |
|
6 |
while(!found && index < list.length) { |
7 |
if(list[index] == value) { |
8 |
found = true; |
9 |
position = index; |
10 |
} else { |
11 |
index += 1; |
12 |
}
|
13 |
}
|
14 |
return position; |
15 |
}
|
Properties of Linear Search
It is important to note that the linear search algorithm does not need to use a sorted list. Also, the algorithm can be customised for use in different scenarios like searching for an array of objects by key. If you have an array of customer data that includes keys for the first and last name, you could test if the array has a customer with a specified first name. In that case, instead of checking if list[index] is equal to our search value, you would check for list[index].first.
Time Complexity of Linear Search
The best-case time complexity is achieved if the element searched is the first element in the list. Now, the search would complete with a single comparison. Hence, the best-case time complexity would be O(1).
The worst-case time complexity occurs if the element searched is the last element or is not present in the list. In this case, the search has to compare all elements in the array. We say that the input data has length n, which means the overall time complexity is O(n) due to the n comparisons made.
In the example above, I used the linearSearch function on an array with eight elements. In the worst case, when the search value is not in the list or is at the end of the list, the function would have to make eight comparisons. Because our array is so small, there is no need to optimise using a different algorithm. However, beyond a certain point, it is no longer efficient to use a linear search algorithm, and that's when using a binary search algorithm would be better.
The average time complexity of linear search is also O(n).
Space Complexity of Linear Search
The overall space complexity of this algorithm is equivalent to the size of the array. Hence, O(n). You don't need to reserve any additional space for completing this algorithm.
Binary Search
Imagine you are playing a number guessing game. You are asked to guess a number between 1 and 100. If your number is too high or too low, you will get a hint.
What would your strategy be? Would you choose numbers randomly? Would you start with 1, then 2, and so on until you guessed correctly? Even if you had unlimited guesses, you want to make the correct guess in as few tries as possible. Therefore, you might start by guessing 50. If the number is higher, you could guess 75. If it is lower, then that means the number is between 50 and 75, and you would choose a number that's in the middle. You would go on like this until you arrived at the correct number. This is similar to how binary search works.
There are two ways of implementing binary search:
- iterative method
- recursive method
Pseudocode for Iterative Binary Search
Here's some pseudocode that expresses the binary search using the iterative method:
1 |
do until the low and high pointers have not met or crossed |
2 |
mid = (low + high)/2 |
3 |
if (x == arr[mid]) |
4 |
return mid |
5 |
else if (x > arr[mid]) |
6 |
low = mid + 1 |
7 |
else |
8 |
high = mid - 1 |
Pseudocode for Recursive Binary Search
Here is the pseudocode for implementing the binary search using the recursive method.
1 |
binarySearch(arr, x, low, high) |
2 |
if low > high |
3 |
return False |
4 |
else |
5 |
mid = (low + high) / 2 |
6 |
if x == arr[mid] |
7 |
return mid |
8 |
else if x > arr[mid] |
9 |
return binarySearch(arr, x, mid + 1, high) |
10 |
else |
11 |
return binarySearch(arr, x, low, mid - 1) |
Regardless of the technique used, the binary search algorithm always uses the divide and conquer approach.
Step-by-Step Explanation
Let's consider an array [1,9,13,16,3,5,0,12] where the searchValue is 13.
We start with a sorted array as required to perform a binary search. Note that sorting the array is expensive, but once it's done, the array can be efficiently searched many times.
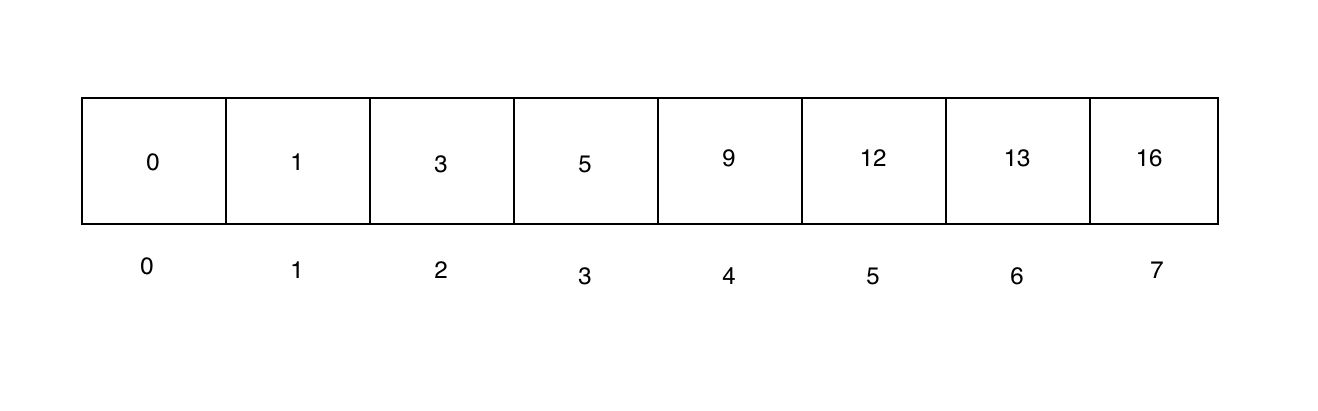
Now, the high and low pointers will be set to the first and last elements respectively. The mid pointer is set to the index given by (low - high) / 2.
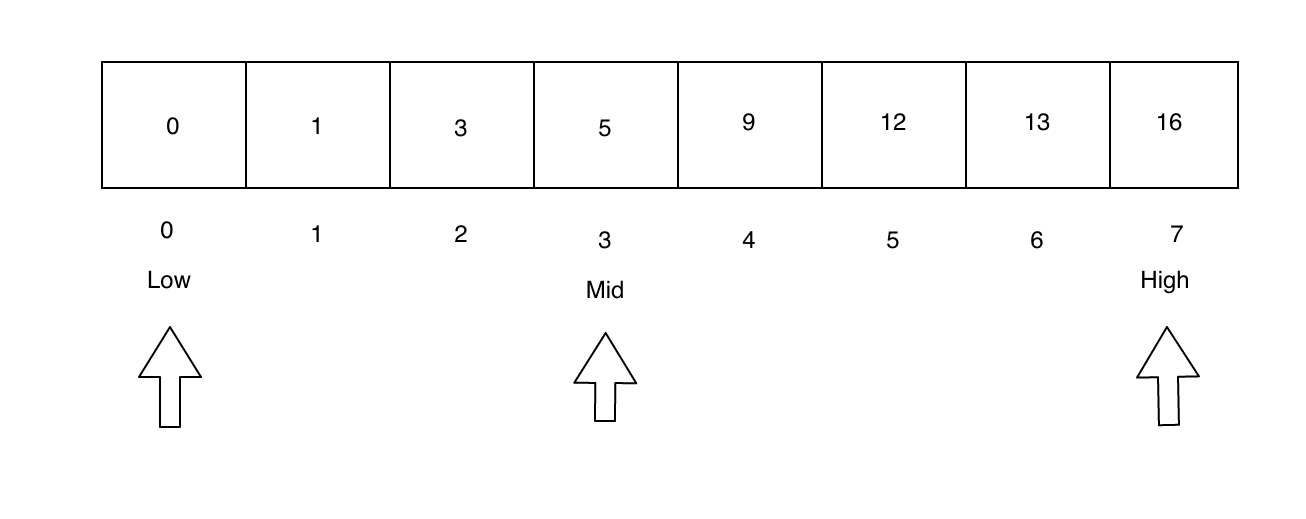
Since searchValue > mid, we need to search the right side of the array. So we set the low pointer to be just after mid, and mid is reset to be between the low and high pointers.
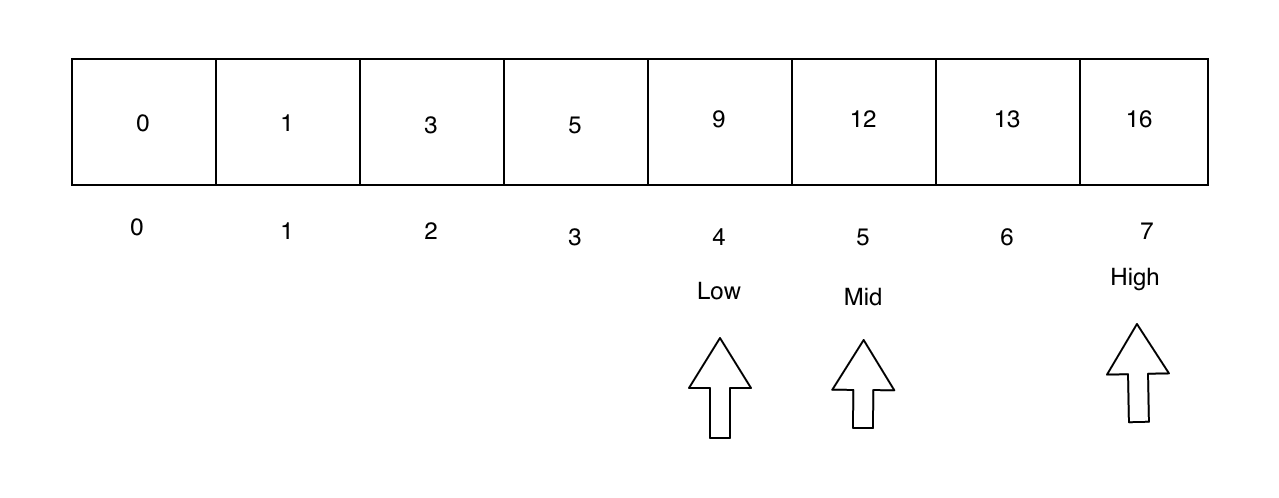
Again, the target value is towards the right of the array. Once again, we adjust the low and high pointers. Now the low and mid pointers are the same.
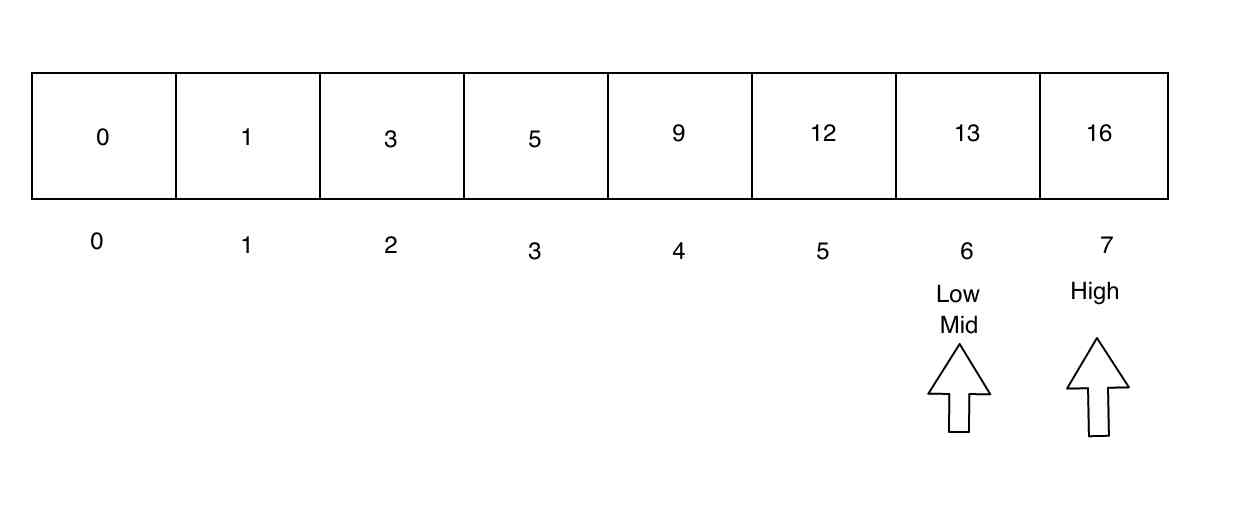
Now, the searchValue is found at mid, which means we have reached the end of our search!
| Step | low |
mid |
high |
list[mid] |
|---|---|---|---|---|
| 1 | 0 |
3 |
7 |
5 |
| 2 | 4 |
5 |
7 |
9 |
| 3 | 6 |
6 |
7 |
13 |
Javascript Implementation of Binary Search
Now let's code the binary search algorithm in JavaScript!
We'll create a function, binarySearch, that accepts a value and an array as parameters. It will return the index where the value occurs in the list if found. If the value is not found, it returns -1. This is our implementation written in JavaScript:
1 |
//note that list must be sorted for this function to work
|
2 |
function binarySearch(value, list) { |
3 |
let low = 0; //left endpoint |
4 |
let high = list.length - 1; //right endpoint |
5 |
let position = -1; |
6 |
let found = false; |
7 |
let mid; |
8 |
|
9 |
while (found === false && low <= high) { |
10 |
mid = Math.floor((low + high)/2); |
11 |
if (list[mid] == value) { |
12 |
found = true; |
13 |
position = mid; |
14 |
} else if (list[mid] > value) { //if in lower half |
15 |
high = mid - 1; |
16 |
} else { //in in upper half |
17 |
low = mid + 1; |
18 |
}
|
19 |
}
|
20 |
return position; |
21 |
}
|
Time Complexity
One of the main reasons why we use binary search for finding elements in an array would be its time complexity. In a best-case scenario, the time complexity for Binary Search is O(1). This happens when the element in the middle of the array matches the search element.
At worst, the time complexity for searching an element using binary search is O(log n)—much less than O(n) for large values of n. To get an idea of how much slower growing log(n) is than n, here is a table of typical values of log(n).
| n | log(n) |
| 1 | 1 |
| 8 | 3 |
| 1024 | 10 |
| 1,000,000 | 19.9 |
| 1,000,000,000,000,000,000 | 59.8 |
So, as you can see, the bigger n gets, the more the improvement of a binary search over a linear search.
The average case time complexity is also O(log n), for searching an item using binary search.
Space Complexity
The space complexity for implementing the binary search is again O(n).
Properties of Binary Search
Unlike linear search, binary search uses a sorted list. That lets us use a "divide and conquer" algorithm to solve the problem.
Conclusion
In this tutorial, we saw how to implement a linear search and a binary search algorithm. The linear search algorithm is simpler and doesn't require a sorted array. However, it is inefficient to use with larger arrays. In the worst case, the algorithm would have to search all elements making n comparisons (where n is the number of elements).
The binary search algorithm, on the other hand, requires you to sort the array first and is more complicated to implement. However, it is more efficient even when considering the cost of sorting. For example, an array with 10 elements would make at most 4 comparisons for a binary search vs. 10 for a linear search—not such a big improvement. However, for an array with 1,000,000 elements, the worst case in binary search is only 20 comparisons. That's a huge improvement over linear search!
Knowing how to use binary search isn't just something to practice for an interview question. It's a practical skill that can make your code work much more efficiently.
This post has been updated with contributions from Divya Dev. Divya is a front-end developer more than half a decade of experience. She is a grad and gold medalist from Anna University.












