Zahlensysteme: Eine Einführung in Binär, Hexadezimal und mehr

German (Deutsch) translation by Ines Willenbrock (you can also view the original English article)

Sahen Sie schon einmal verrückte binäre Zahlen und fragten sich, was sie meinten? Sahen Sie schon einmal Zahlen mit Buchstaben gemischt und fragten sich, was los ist? All dies und mehr erfahren Sie in diesem Artikel. Hexadezimal muss nicht beängstigend sein.

(Danke an das ReBoot Wiki für das Miniaturbild.)

Einleitung: Was ist ein Zahlensystem?

Sie wissen wahrscheinlich schon, was ein Zahlensystem ist - Sie haben sicherlich von binären Zahlen oder hexadezimalen Zahlen gehört? Einfach ausgedrückt, ist ein Zahlensystem eine Möglichkeit, Zahlen darzustellen. Wir sind daran gewöhnt, das Basis-10-Zahlensystem zu verwenden, das auch als Dezimal bezeichnet wird. Andere gängige Zahlensysteme sind Basis-16 (Hexadezimal), Basis-8 (Oktal) und Basis-2 (Binär).

In diesem Artikel erkläre ich, was diese verschiedenen Systeme sind, wie man mit ihnen arbeitet und warum das Wissen über sie Ihnen helfen wird.

Aktivität

Bevor wir anfangen, wollen wir zum Spaß eine kleine Aktivität durchführen. Es gibt viele verschiedene Möglichkeiten, eine Farbe darzustellen, aber eine der häufigsten ist das RGB-Farbmodell. Bei diesem Modell besteht jede Farbe aus einer Kombination verschiedener Mengen an Rot, Grün und Blau.

Sie fragen sich vielleicht, wie Farben zu Zahlensystemen stehen. Kurz gesagt, auf einem Computer wird jede Farbe als große Zahl gespeichert: eine Kombination aus Rot, Grün und Blau. (Wir werden später näher darauf eingehen.) Da es sich nur um eine Zahl handelt, kann es auf verschiedene Weise mit unterschiedlichen Zahlensystemen dargestellt werden.

Ihre Aufgabe ist es zu erraten, wie viel Rot, Grün und Blau in der Hintergrundfarbe der Aktivität unten ist. Die Werte für Rot, Grün und Blau können zwischen 0 und 255 liegen.

Nutzen Sie die verschiedenen Hinweise, die Ihnen zur Verfügung stehen. Wenn Sie die numerischen Hinweise noch nicht verstehen, kein Problem! Sie können sehen, wie Ihre Vermutung aussieht, indem Sie die Schaltfläche Tipp anzeigen verwenden. Im Moment mag es schwierig erscheinen, aber am Ende dieses Artikels wird es hoffentlich einfach erscheinen.

Blick auf Basis-10

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11... Sie haben Ihr ganzes Leben lang in Basis-10 gezählt. Schnell, was ist 7+5? Wenn Sie 12 beantwortet haben, denken Sie in Basis-10. Werfen wir einen genaueren Blick auf das, was Sie all die Jahre gemacht haben, ohne jemals darüber nachzudenken.

Werfen wir einen kurzen Blick auf das Zählen. Zuerst gehen Sie alle Ziffern durch: 0, 1, 2... Sobald Sie 9 erreicht haben, haben Sie keine Ziffern mehr, um die nächste Zahl darzustellen. Sie ändern es also wieder auf 0, und fügen 1 zur Zehnerziffer hinzu, sodass Sie 10 haben. Der Vorgang wiederholt sich immer wieder, und schließlich gelangen Sie zu 99, wo Sie keine größeren Zahlen mit zwei Ziffern erstellen können, so dass Sie eine weitere hinzufügen, so dass Sie 100 haben.

Obwohl das alles sehr einfach ist, sollten Sie nicht übersehen, was vor sich geht. Die rechte Ziffer stellt die Anzahl der Ziffern dar, die nächste Ziffer stellt die Anzahl der Zehner, die nächste die Anzahl der Hunderte usw. dar.

Visualisierung von Basis-10

Verwirrt durch diese Beschreibungen? Kein Problem - unten ist eine Demo, um Ihnen zu helfen. Geben Sie einfach eine Zahl in das Textfeld ein und klicken Sie auf Zeichnen. Versuchen Sie, eine große Zahl einzugeben, z. B. 2347. Sie sehen 2 Gruppen von tausend, 3 Gruppen von hundert, 4 Gruppen von zehn und 7 einzelne Blöcke.

Basis-10 mathematisch

Möglicherweise haben Sie inzwischen ein Muster bemerkt. Schauen wir uns das, was mathematisch vor sich geht, am Beispiel von 2347 an.

Wie Sie gesehen haben, gibt es 2 Gruppen von Tausend. Nicht zufällig 1000 = 10*10*10, die auch als 10³ geschrieben werden können.
Es gibt 3 Gruppen von Hundert. Wieder, nicht zufällig, 100 = 10*10 oder 10².
Es gibt 4 Gruppen von Zehn, und, 10 = 10¹.
Schließlich gibt es 7 Gruppen von Eins, und 1 = 10⁰. (Das mag seltsam erscheinen, aber jede Zahl hoch 0 entspricht per Definition 1.)

Dies ist im Wesentlichen die Definition von Basis-10. Um den Wert einer Zahl in Basis-10 zu erhalten, folgen wir einfach diesem Muster. Hier sind ein paar weitere Beispiele:

892 = 8 *10²+9*10¹+2*10⁰
1147 = 1*10³+1*10²+4*10¹+7*10⁰
53 = 5 *10¹+3*10⁰

Zugegeben, das alles scheint ein wenig albern. Wir alle wissen, welchen Wert eine Basis-10-Zahl hat, weil wir immer Basis-10 verwenden, und es für uns natürlich ist. Wie wir jedoch bald sehen werden, können wir andere Basen besser verstehen, wenn wir die Muster im Hintergrund von Basis-10 verstehen.

Basis-8

Auf zu Basis-8, auch Oktal genannt. Basis-8 bedeutet genau das, was klingt: Das System basiert auf der Zahl acht (im Gegensatz zu zehn). Erinnern Sie sich, wie wir in Basis-10 zehn Ziffern hatten? Jetzt, in Basis-8, sind wir auf nur acht Ziffern beschränkt: 0, 1, 2, 3, 4, 5, 6 und 7. Es gibt keine 8 oder 9.

Wir zählen genauso wie normalerweise, außer mit nur acht Ziffern. Anstelle einer ausführlichen Erklärung probieren Sie einfach die Demo unten aus, indem Sie auf "1 hochzählen" klicken, um zu sehen, wie das Zählen in Basis-8 funktioniert.

Sie sollten ein ähnliches Muster wie zuvor bemerken; nachdem wir bis 7 gekommen sind, gehen uns die verschiedenen Ziffern für jede höhere Zahl aus. Wir brauchen einen Weg, um acht von etwas zu repräsentieren. Also fügen wir eine weitere Ziffer hinzu, ändern die 7 zurück auf 0 und landen bei 10. Unsere Antwort von 10 in Basis-8 stellt nun dar, was wir normalerweise als 8 in Basis-10 denken würden.

Das Sprechen über Zahlen, die in mehreren Basen geschrieben sind, kann verwirrend sein. Zum Beispiel, wie wir gerade gesehen haben, 10 in Basis-8 ist nicht das gleiche wie 10 in Basis-10. Von diesem Zeitpunkt an verwende ich also eine Standardnotation, in der ein Subskript bei Bedarf die Basis von Zahlen bezeichnet. Zum Beispiel sieht unsere Basis-8-Version von 10 jetzt wie 10₈ aus.

(Anmerkung der Redaktion: Ich finde es viel einfacher, dies zu verstehen, wenn ich die Art und Weise, wie ich diese Zahlen in meinem Kopf lese, auch ändere. Zum Beispiel für 10₈ lese ich "Oktal eins-null" oder "eins-null in Basis-acht". Für 10₁₀ lese ich "Dezimal eins-null" oder "eins-null in Basis-zehn".)

Großartig, nun wissen wir, dass 10₈ acht Elemente dar stellt. (Sie können immer eine Zahl in das erste Werkzeug einfügen, um eine Visualisierung zu erhalten) Was ist die nächste Zahl nach 77₈? Wenn Sie 100₈ gesagt haben, haben Sie Recht. Wir wissen aus dem, was wir bisher gelernt haben, dass die ersten 7 in 77₈ Gruppen von 8 und die zweite 7 für einzelne Elemente stehen. Wenn wir diese alle addieren, haben wir 7 *8 + 7*1 = 63. Wir haben also insgesamt 63₁₀. Also 77₈=63₁₀. Wir alle wissen, dass 64₁₀ nach 63₁₀ kommt.

Konvertieren von Basis-8 zu Basis-10

Schauen wir uns jetzt ein wortreicheres Beispiel an. John bietet Ihnen 47₈ Cookies und Jane bietet an, Ihnen 43₁₀ Cookies zu geben. Wessen Angebot nehmen Sie an? Wenn Sie möchten, fahren Sie fort und generieren Sie die Grafik für 47₈ Grafik mit dem ersten Werkzeug. Lassen Sie uns seinen Basis-10-Wert herausfinden, so dass wir die beste Entscheidung treffen können!

Wie wir beim Zählen gesehen haben, stellen die vier von 47₈ die Anzahl der Gruppen von acht dar. Das macht Sinn - wir befinden uns in der Basis-8. Insgesamt haben wir also vier Gruppen von acht und sieben Gruppen von einem. Wenn wir diese alle addieren, erhalten wir 4 *8 + 7*1 = 39₁₀. Also, 47₈ Cookies ist genau das gleiche wie 39₁₀ Cookies. Janes Angebot scheint jetzt das beste zu sein!

Das Muster, das wir vorher mit Basis-10 gesehen haben, gilt auch hier. Schauen wir uns 523₈ an. Es gibt fünf Gruppen von 8², zwei Gruppen von 8¹ und drei Gruppen von 8⁰ (erinnern Sie sich, 8⁰=1). Rechnet man diese alle zusammen, 5*8² + 2*8¹ + 3*8⁰ = 5*64+2*8+3 = 339, erhalten wir 339₁₀, was unsere letzte Antwort ist. Das folgende Diagramm zeigt das Gleiche visuell:

Hier sind ein paar weitere Beispiele:

111₈ = 1*8²+1*8¹+1*8⁰ = 64+8+1 = 73₁₀
43₈ = 4*8¹+3*8⁰ = 32+3 = 35₁₀
6123₈= 6*8³+1*8²+2*8¹+3*8⁰ = 3072+64+16+3 = 3155₁₀

Konvertieren von Basis-10 zu Basis-8

Die Konvertierung von Basis-10 zu Basis-8 ist etwas schwieriger, aber immer noch unkompliziert. Grundsätzlich müssen wir den Prozess von oben umkehren. Beginnen wir mit einem Beispiel: 150₁₀.

Wir finden zunächst die größte Potenz von 8, die kleiner ist als unsere Zahl. Hier sind es 8² oder 64 (8³ ist 512). Wir zählen, wie viele Gruppen von 64 wir von 150 nehmen können. Dies ist 2, also ist die erste Ziffer in unserer Basis-8-Zahl 2. Wir haben jetzt 128 von 150 ausgemacht, also haben wir 22 übrig.

Die größte Potenz von 8, die kleiner als 22 ist, ist 8¹ (d. h. 8). Wie viele Gruppen von 8 können wir von 22 nehmen? Zwei Gruppen wieder, und damit ist unsere zweite Ziffer 2.

Schließlich haben wir 6 über, und können offensichtlich 6 Gruppen von einer aus dieser, unsere letzte Ziffer, nehmen. Am Ende sind es 226₈.

In der Tat können wir diesen Prozess einen Hauch klarer mit Mathematik machen. Hier sind die Schritte:

150/8² = 2 Rest 2
22/8¹ = 2 Rest 6
6/8⁰ = 6

Unsere endgültige Antwort ist dann die Gesamtheit der nicht verbleibenden Ziffern, also 226. Beachten Sie, dass wir immer noch beginnen, indem wir durch die höchste Potenz von 8 dividiert, die kleiner als unsere Zahl ist.

Umgang mit einer beliebigen Basis

Es ist wichtig, die Konzepte, die wir über Basis-8 und Basis-10 gelernt haben, auf jede Basis anwenden zu können. Genauso wie Basis-8 acht Ziffern und Basis-10 zehn Ziffern hatte, hat jede Basis die gleiche Anzahl von Ziffern wie ihre Basis. So hat Basis-5 fünf Ziffern (0-4), Basis-7 sieben Ziffern (0-6), etc.

Sehen wir uns nun an, wie Sie den Wert zur Basis 10 einer beliebigen Zahl in einer beliebigen Basis finden. Angenommen, wir arbeiten in Basis-b, wo b eine beliebige positive ganze Zahl sein kann. Wir haben eine Nummer d₄d₃d₂d₁d₀, wobei jedes d eine Ziffer in einer Zahl ist. (Die Subskriptionen beziehen sich hier nicht auf die Basis der Zahl, sondern differenzieren einfach jede Ziffer.) Unser Basis-10-Wert ist einfach d₄*b⁴ + d₃*b³ + d₂*b² + d₁*b¹ + d₀*b⁰.

Hier ist ein Beispiel: Wir haben die Nummer 32311 in Basis-4. Beachten Sie, dass unsere Zahl nur Ziffern von null bis drei hat, da Basis-4 nur vier Gesamtziffern hat. Unser Basis-10-Wert ist 3*4⁴ + 2*4³ + 3*4² + 1*4¹ + 1*4⁰ = 3*256 + 2*64 + 3*16 + 1*4 + 1*1 = 949. Wir könnten, natürlich, diesem Muster mit einer beliebigen Anzahl von Ziffern in unserer Nummer folgen.

Basis-16

Basis-16 wird auch Hexadezimal genannt. Es wird häufig in der Computerprogrammierung verwendet, daher ist es sehr wichtig zu verstehen. Beginnen wir mit der Zählung in Hexadezimal, um sicherzustellen, dass wir das, was wir bisher über andere Basen gelernt haben, anwenden können.

Da wir mit Basis-16 arbeiten, haben wir 16 Ziffern. Also, wir haben 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ... und yikes! Uns sind die Ziffern ausgegangen, aber wir brauchen noch sechs weitere. Vielleicht könnten wir so etwas wie eine eingekreiste 10 verwenden?

Die Wahrheit ist, wir könnten, aber das wäre ein Graus zu tippen. Stattdessen verwenden wir einfach Buchstaben des Alphabets, beginnend mit A und weiter zu F. Hier ist eine Tabelle mit allen Ziffern von Basis-16:

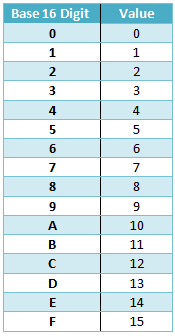
Abgesehen von diesen zusätzlichen Ziffern ist Hexadezimal wie jede andere Basis. Konvertieren wir z. B. 3D₁₆ nach Basis-10. Nach unseren bisherigen Regeln haben wir: 3D₁₆ = 3*16¹ + 13*16⁰ = 48 + 13 = 61. 3D₁₆ entspricht also 61₁₀. Beachten Sie, wie wir den Wert von D von 13 in unserer Berechnung verwenden.

Wir können von Bais-10 zu Basis-16 konvertieren, ähnlich wie wir es mit Basis-8 gemacht haben. Konvertieren wir 696₁₀ in Base-16. Erstens finden wir die größte Potenz von 16, die kleiner als 696₁₀ ist. Das sind 16² oder 296. Dann:

696/16² = 2 Rest 184
184/16¹= 11 Rest 8
8/16¹ = 8 Rest 0

Wir müssen 11 durch die Zifferndarstellung B ersetzen, und wir erhalten 2B8₁₆.

Fühlen Sie sich frei, zur Übung einige weitere Konvertierungen zu versuchen. Sie können die untenstehende Anwendung verwenden, um Ihre Antworten zu überprüfen:

Binär! (Basis-2)

Auf zur berühmten Basis-2, auch Binär genannt. Während jeder weiß, dass Binär aus 0en und 1en besteht, ist es wichtig zu verstehen, dass es mathematisch nicht anders ist als jede andere Basis. Es gibt einen alten Witz, der so geht:

Können Sie herausfinden, was es bedeutet?

Lassen Sie uns ein paar Konvertierungen mit Basis-2 versuchen. Zuerst konvertieren wir 101100₂ in Base-10. Wir haben: 101100 = 1*2⁵ + 1*2³ + 1*2² = 32 + 8 + 4 = 44₁₀.

Konvertieren wir nun 65 in Binär. 2⁶ ist die höchste Potenz von 2 kleiner als 65, also:

65/2⁶ = 1 Rest 1
1/2⁵ = 0 Rest 1
1/2⁴ = 0 Rest 1
1/2³ = 0 Rest 1
1/2² = 0 Rest 1
1/2¹ = 0 Rest 1
1/2⁰ = 1 Rest 0

Und so erhalten wir unsere binäre Zahl, 1000001.

Das Verständnis des Binärsystems ist super wichtig. Ich habe unten eine Tabelle aufgenommen, um auf die Werte von Ziffern hinzuweisen.

Der Wert 10001 ist z. B. 17, was die Summe der Werte der beiden 1 Ziffern (16+1) ist. Das ist nichts anderes als wir es vorher getan haben, es ist nur in einer leicht lesbaren Weise präsentiert.

Tricks und Tipps

Normalerweise würden Sie beim Konvertieren zwischen zwei Basen, die nicht Basis-10 sind, etwas wie folgt tun:

Zahl nach Basis-10 konvertieren
Ergebnis in die gewünschte Basis konvertieren

Es gibt jedoch einen Trick, mit dem Sie schnell zwischen Binär und Hexadezimal konvertieren können. Nehmen Sie zunächst eine beliebige binäre Zahl und teilen Sie ihre Ziffern in Vierergruppen auf. Also, sagen wir, wir haben die Nummer 1011101₂. Aufgeteilt haben wir 0101 1101. Beachten Sie, wie wir einfach zusätzliche Nullen zur Vorderseite der ersten Gruppe hinzufügen können, um gleichmäßige Gruppen von 4 zu bilden. Wir finden jetzt den Wert für jede Gruppe, als ob es ihre eigene separate Nummer wäre, was uns 5 und 13 gibt. Schließlich verwenden wir einfach die entsprechenden hexadezimalen Ziffern, um die Basis-16-Zahl 5D₁₆ zu schreiben.

Wir können auch in die andere Richtung gehen, indem wir jede hexadezimale Ziffer in vier binäre Ziffern umwandeln. Versuchen Sie, B7₁₆ nach Binär zu konvertieren. Sie sollten 10110111₂ erhalten.

Dieser Trick funktioniert, weil 16 eine Potenz von 2 ist. Das bedeutet, dass wir einen ähnlichen Trick für Base-8 verwenden, was auch eine Potenz von 2 ist:

Natürlich können Sie den Prozess umkehren, um von Basis-8 zu Binär zu gehen.

Schlussfolgerung

Lassen Sie uns den ganzen Weg zurück gehen und das Farbraten-Spiel noch einmal besuchen.

In Flash werden Farben als einzelne Zahl gespeichert. Wenn die ersten beiden Ziffern nach Hexadezimal konvertiert werden, stellen sie die Menge an Rot, die nächsten beiden die Menge an Grün und die letzten beiden die Menge an Blau dar. Wenn unsere Farbe also 17FF18₁₆ ist, können wir leicht feststellen, dass unsere rote Komponente 17₁₆ oder 23₁₀ ist. Unsere grüne Komponente ist FF₁₆ oder 255₁₀. Schließlich ist unsere blaue Komponente 18₁₆ oder 24₁₀. Wenn wir die Basis-10-Version unserer Farbe, 1572632₁₀, erhalten, müssen wir sie in Hexadezimal konvertieren, bevor wir etwas darüber sagen können.

Versuchen Sie das Spiel noch einmal, und sehen, wie viel besser Sie sein können!

Das Verständnis unterschiedlicher Nummernsysteme ist in vielen computerbezogenen Bereichen äußerst nützlich. Binär und Hexadezimal sind sehr häufig, und ich ermutige Sie, sich mit ihnen sehr vertraut zu machen. Vielen Dank für das Lesen - ich hoffe, Sie haben viel aus diesem Artikel gelernt! Fühlen Sie sich frei, den Quellcode von einer der Demos zu greifen. Wenn Sie Fragen haben, stellen Sie diese bitte unten.